Сложность алгоритмов
Такая вот интересная сложность – Введение в алгоритмическую сложность
Оригинал - http://algosaur.us/algorithmic-complexity/ от radhika
Неплохо знать что такое:
- Степень
- Алгебра вообще
- Функции и асимптоты
- Сортировка вставками (на уровне алгоритма) и вообще сортировки
Этот пост можно грубо разделить на 3 части, так что можете выбрать сразу любую, в зависимости от скилла:
Алгоритмическая сложность и рост функций составляют самую основу алгоритмов. Они дают нам представление о том, насколько алгоритм быстрый или медленный, так что вы не сможете разрабатывать и анализировать алгоритмы, не зная про сложность.

Алгозавру очень хочется узнать что такое “рост функции”. И для этого он решил завести двух кроликов. А где два кролика, там… много кроликов. Усредним количество потомства с каждой пары до четырёх (не будем уточнять каким образом).
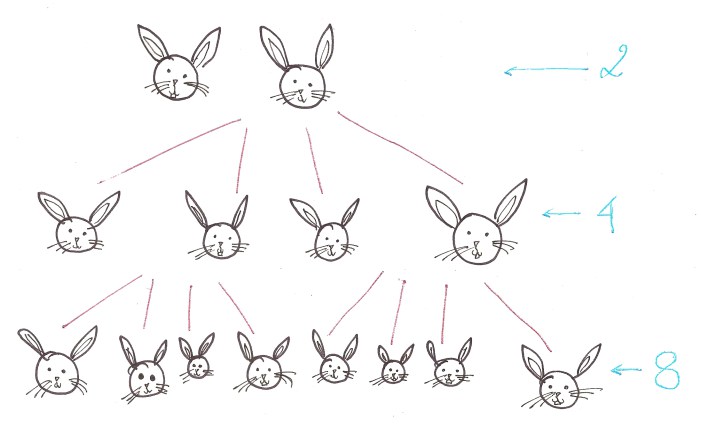
Если мы задумаем посчитать скорость роста количества кроликов, у нас получится 2^n, где n - номер поколения. Это не очень хорошая новость для Алгозавра, ибо сколь бы ни были кролики няшными - в какой-то момент их будет слишком много.

Грубо говоря, сложность алгоритма разведения кроликов равна O(2^n).
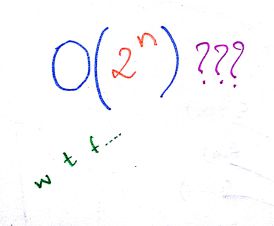
Поскольку количество кролей в следующем поколении растёт экспоненциально в зависимости от начального их количества (или, на языке алгоритма - входных данных).
Давайте это разберём.
“Порядок роста времени работы алгоритма является простейшей характеристикой эффективности алгоритма, и даёт возможность сравнить его по сложности с другими алгоритмами” (Святое Евангелие от CLRS)
Представим, что Алгозавр спускается вниз по очень странной лестнице с n ступеньками. Чтобы спуститься вниз на одну ступеньку, он должен пройти по ней n шагов горизонтально, и только потом вниз.
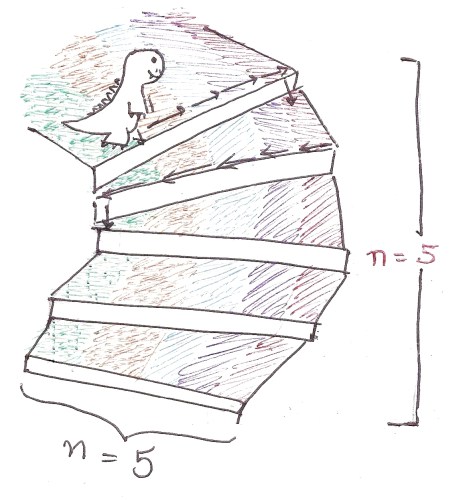
Так что на каждой ступеньке он должен сделать n шагов. И для n ступенек всего он должен пройти n^2 шагов.
def weirdStairs(nofStairs):
steps = 0
for i in range(0, nofStairs):
steps += nofStairs
steps += 1
print stepsСколько времени займёт весь спуск?

Аналогично давайте рассмотрим сортировку вставкой.
def insertionSort(list):
for i in range(1, len(list)):
currentValue = list[i]
position = index
while position > 0 and list[position - 1] > currentValue:
list[position] = list[position - 1]
list[position] = currentValueПредположим наихудший вариант - список отсортирован в обратном порядке, т.е. каждая строчка кода в цикле выполнится для каждого элемента.
Как видно по коду, каждый элемент в списке передвинет все остальные элементы.
Если длина списка - n, то эффективность не будет линейно пропорциональна n, но будет пропорциональна n в квадрате.
Так что в худшем случае время работы алгоритма сортировки вставкой будет примерно равно O(n^2), где О - стандартное обозначение, а n - количество элементов в списке.
Для измерения эффективности нас интересует только худший вариант.
Пока что мы сортировали только списки из 10, максимум 100 элементов. Что, если их будет 1000? 1 000 000? Например количество пользователей Вконтакте?
Да, в таком случае алгоритмическая сложность действительно важна.В этих примерах количество элементов настолько большое, что имеет значение только наивысшая степень. Остальные числа не важны.
Приоритет порядков роста функции примерно такой:

Грубо говоря, мы можем считать сложность алгоритма по одной только структуре циклов в нём.
Проход по циклу даёт O(n), как и подсчёт его длины. Из чего следует, что время работы пропорционально количеству элементов.
def traversal(list):
for i in range(len(list)):
print list[i]Теперь Алгозавр знает достаточно много о росте функции, чтобы понять какой алгоритм быстрее. Юпиии!
Если хотите понять анализ сложности ещё глубже - читайте дальше. Или сварганьте кофейка, и возвращайтесь когда уляжется всё то, что вы уже прочитали. Можете оставить закладку прямо тут.
Открыв CLRS на 43 странице, Алгозавр увидел…

Давайте сперва выясним, что такое “асимптотическая нотация”. Как вы возможно знаете, когда аргумент функции близится к бесконечности, её значение приближается к некой линии, но никогда её не касается. Эта линия называется асимптотой.
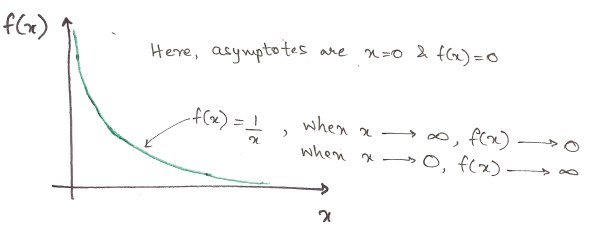
Вас это должно интересовать, поскольку разрабатывая алгоритм, Вам нужно знать как он работает на огромных числах. Вы уже знаете про О-нотацию: она показывает эффективность в самом худшем случае. Давайте перейдём к Ω. Я опять возьму в качестве примера сортировку. Но теперь входной список уже отсортирован как надо, т.е. это наилучший случай работы алгоритма.
def insertionSort(someList):
for i in range(1, len(someList)):
currentValue = someList[i]
position = i
while position > 0 and someList[position - 1] > currentValue:
someList[position] = someList[position - 1]
position -= 1
someList[position] = currentValue
return someListМы всё равно должны пройти список один раз, даже если нам не придётся заходить во вложенный цикл. Внешний цикл отработает n раз.
Так что в наилучшем случае сложность этого алгоритма - Ω(n).
Чтобы понять что означают другие богом забытые символы, нам придётся вспомнить алгебру…
Функции! И графики с ними!
Формально мы можем определить Θ, O, и Ω вот так:
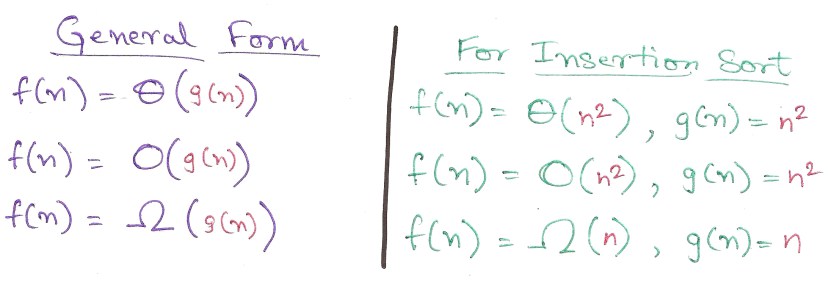
Если честно, понятнее не стало. Подключаем тяжёлую артиллерию: графики. (срисованы с 45 страницы CLRS)
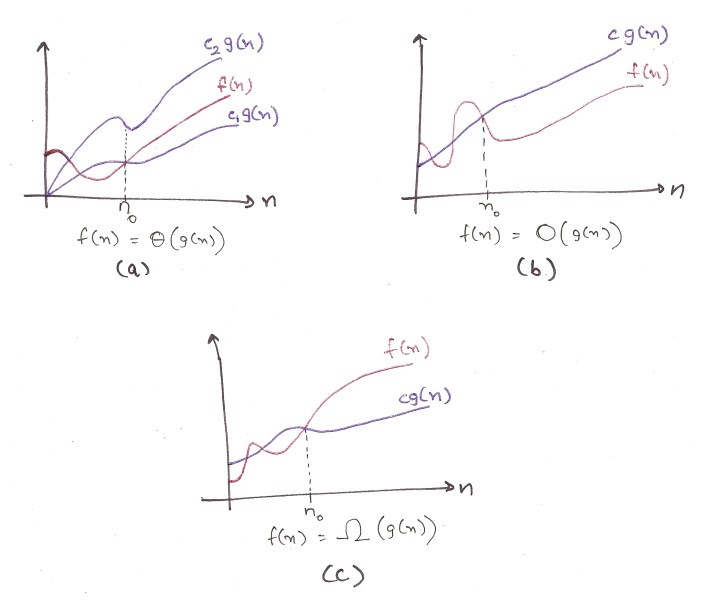
Несколько тонкостей. Эти функции должны быть монотонны на множестве аргументов, начиная с n_0.
Например Ω(g(n)) определена только тогда, когда она меньше времени работы (c*g(n)) для всех n > n_0.
a) Это график Θ. Он выглядит как котлета в гамбургере между двумя функциями, что показывает, что Θ(g(n)) определена только между верхей и нижней границами. Попробуйте доказать.
b) Это график О. Время работы функции всегда меньше O(g(n)), что подтверждает, что О является верхней границей сложности. Хуже эффективности быть не может.
c) для Ω. The Время работы функции всегда больше Ω(g(n)), и это лучший случай. Большей эффективности от алгоритма не ждите.
Терпение, мой друг. Вот практический смысл всего этого:
1. Ω полезен, когда нужно узнать самый быстрый вариант работы.
Ну, иногда это полезно.
2. О покажет самый худший вариант работы алгоритма.
Вот это интересно всегда.
3. Найти Θ сложнее чем О, так что О используют чаще. Математики скажут что это не кошерно, но пусть считают его сами.
Фух, на этом всё с теорией.
Автор оригинала оставил адрес: rawrr@algosaur.us
Литература:
Дасгупта С., Пападимитриу Х., Вазирани У. Алгоритмы.
Numbers: The Key to the Universe – Kjartan Poskitt (Пример про кроликов взят оттуда)